练习：迭代方法

在这节课中到目前为止，我们讨论了智能体可以如何获得策略 \pi 对应的状态值函数 v_\pi。

在动态规划设置中，智能体完全了解马尔可夫决策流程 (MDP)。在这种情况下，可以使用 MDP 的一步动态 p(s',r|s,a) 获得 v_\pi 的贝尔曼期望方程对应的方程组。

在网格世界示例中，等概率随机策略对应的方程组由以下方程获得：

v_\pi(s_1) = \frac{1}{2}(-1 + v_\pi(s_2)) + \frac{1}{2}(-3 + v_\pi(s_3))

v_\pi(s_2) = \frac{1}{2}(-1 + v_\pi(s_1)) + \frac{1}{2}(5 + v_\pi(s_4))

v_\pi(s_3) = \frac{1}{2}(-1 + v_\pi(s_1)) + \frac{1}{2}(5 + v_\pi(s_4))

v_\pi(s_4) = 0

为了获得状态值函数，我们只需求解该方程组。

虽然也许始终可以直接求解方程组，但是我们将改用迭代方法。

迭代方法

迭代方法先对每个状态的值进行初始猜测。尤其是，我们先假设每个状态的值为 0。

然后，循环访问状态空间并通过应用连续的更新方程修改状态值函数的估算结果。

注意，V 表示状态值函数的最新猜测，更新方程为：

V(s_1) \leftarrow \frac{1}{2}(-1 + V(s_2)) + \frac{1}{2}(-3 + V(s_3))

V(s_2) \leftarrow \frac{1}{2}(-1 + V(s_1)) + \frac{1}{2}(5)

V(s_3) \leftarrow \frac{1}{2}(-1 + V(s_1)) + \frac{1}{2}(5)

练习问题

假设状态值函数的最新猜测如下图所示。

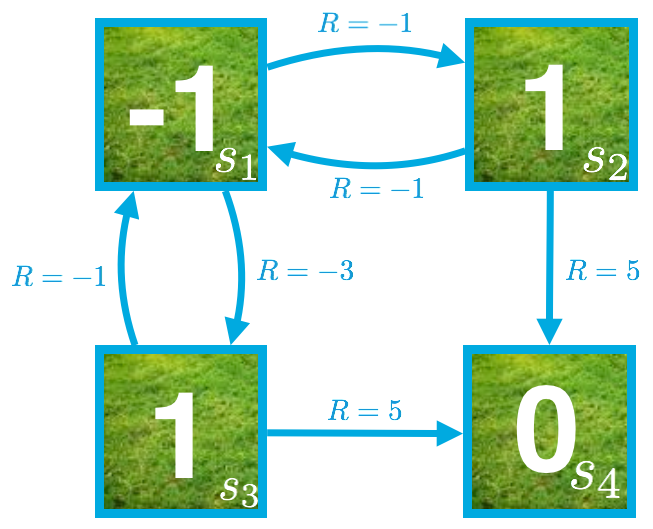
目前，v_\pi(s_2) 的估算结果由 V(s_2) = 1 给出。

假设该算法的下一步是更新 V(s_2)。

应用一次更新步骤后，V(s_2) 的新值是多少？